5.2 图的概念★1◎2

5.2 图的概念★1◎2

　　图由顶点和边的集合组成，定义V为顶点的有穷非空集合，E为连接V中顶点的边的有穷集合，那么定义图G的二元组为：

G=(V,E)

　　1．有向图
　　每条边都是有方向的图叫做有向图。有向图的边都是从一个顶点出发到另一个顶点结束，其中有向图的边称为“弧”，弧的起始点称为“弧尾”，弧的终点称为“弧头”，弧常用尖括号“< >”表示。如图5-1（a）所示。
　　顶点：V={v1,v2,v3,v4}
　　弧：　E={<v1,v2>，<v1,v4>，<v1,v3>，<v2,v4>，<v4,v1>}
　　对于弧<v1,v4>，弧尾是v1，弧头是v4，但对于弧<v4,v1>，弧尾是v4，弧头是v1。因此在有向图5-1（a）中，<v1,v4>和<v4,v1>是两条不同的边。

　　图5-1 图的示意图
　　2．无向图
　　每条边都是没有方向的图叫做无向图，无向图的边用括号“( )”表示，如图5-1(b)所示。
　　顶点：V={v1,v2,v3,v4}
　　边：　E={(v1,v2)，(v1,v4)，(v1,v3)，(v2,v4)}
　　在无向图中，(v1,v4)和(v4,v1)表示同一条边。
　　
　　3．图的顶点和边
　　定义图G中，顶点数为n，边数（弧数）为e，如图5-1(a)中，有向图G有4个顶点，5条边；图5-1(b)中，无向图G有4个顶点，4条边。不考虑从自身连接自身的边或弧有以下几种情况：
　　（1）无向图G的边数e与顶点数n存在关系：

0≤e≤n(n-1)/2

　　即n个顶点的无向图，最多只有“n(n-1)/2”条边，我们把具有“n(n-1)/2”条边的无向图称为“完全图”。
　　（2）有向图G的弧数e与顶点数n存在关系：

0≤e≤n(n-1)

　　即n个顶点的有向图，最多只有“n(n-1)”条边，我们把具有“n(n-1)”条边的有向图称为“有向完全图”。
　　（3）存在没有边或弧的图，也存在边或弧数很少的图，我们称之为“稀疏图”。同理，也存在边或弧很多的图，我们称之为“稠密图”。
　　（4）“网”是指带权的图，“权”是指一个与边或弧相关联的数值，这个数值一般表示该条边或弧之间的距离或耗费等信息，比如AOE图中的权值是指每条边代表的天数。
　　（5）顶点v的“度”是指与V相关联的边或弧的数量，记为TD(v)，比如图5-1(b)中顶点v1，v2，v3，v4的度分别为：3、2、1、2。
　　在有向图中，顶点v的“出度”是指以v为弧尾的弧数量，记为OD(v)，顶点v的“入度”是指以v为弧头的弧的数量，记为ID(v)，顶点v的度等于其入度与出度之和：
　　TD(v) = OD(v) + ID(v)
　　比如图5-1(a)中顶点v1，v2，v3，v4的出度分别为：3，1，0，1；入度分别为：1，1，1，2；度分别为：4，2，1，3。
　　在图G中，所有顶点的度之和为边的两倍，即具有n个顶点，e条边的图，存在关系：

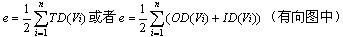
　　如果另一图存在顶点集合V1和边（或弧）集合E1，如果从图G中抽取一部分顶点和边（或弧）组成一个新的图G1（边或弧的两个顶点必须同时抽取），那么称图G1是图G的“子图”，用数学的方法定义如下：
　　存在两个图G=(V,{E})和G1＝(V1,{E1})，如果V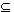1V并且E1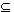E，则称G1为G的子图。
　　4．图的路径与连通
　　定义“路径”为两个顶点之间的一串顶点序列，其中序列中相连的两个顶点之间都存在一条边或弧，比如图5-1(b)中顶点v2到v3之间存在一条路径（v2,v1,v3）。在有向图中路径是有向的，比如图5-1(a)从顶点v2到v3之间存在一条路径（v2,v4,v1,v3）。
　　路径的“长度”是路径上边或弧的数量。
　　“回路”或者“环”是指第一个顶点和最后一个顶点相同的路径。
　　“简单路径”是指没有相同顶点重复出现的路径。
　　在无向图中，如果存在一条连接两个顶点的路径，则称这两个顶点是“连通”的。如果图中任意两个顶点均连通，则称此图为“连通图”，其中无向图中的极大连通子图称为“连通分量”。
　　在有向图中，如果图中任意两个顶点vi和vj（ij），无论是vi到vj，还是从vj到vi，均存在路径，则称此图为“强连通图”，有向图的极大连通子图称为“强连通分量”。
　　“生成树”是连通图的一个极小连通子图，这个子图包含了原图的所有顶点，但是只有n-1条边（n是图的顶点数），即生成树的任意两个顶点之间有且仅有一条路径。